|
| № |
Условие |
Решение
|
Наличие |
| 69055 |
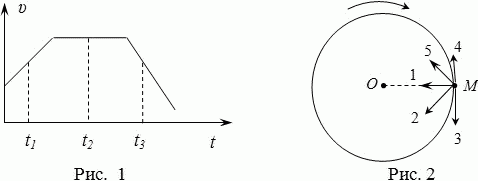
Материальная точка M движется по окружности со скоростью v. На рис. 1 показан график зависимости модуля скорости от времени. При этом вектор полного ускорения в момент времени t3 на рис.2 имеет направление ...
 |
40 руб
оформление Word |
word | | 69056 |
На носу лодки длиной l = 1,5 м стоит человек, держа на высоте h = 1 м камень массой m = 1 кг. Человек бросает камень горизонтально вдоль лодки. Какую скорость относительно берега должен сообщить человек камню, чтобы попасть в корму лодки? Масса лодки с человеком равна M = 250 кг, сопротивление воды и воздуха не учитывать. |
43 руб
оформление Word |
word | | 69057 |
При взрыве атомной бомбы создаются условия для осуществления следующей реакции: 1Н2 + 1Н3 → X + 0n1. Ядро какого элемента образуется при этом? |
40 руб
оформление Word |
word | | 69058 |
Материальная точка равноускоренно двигается по прямой. В момент времени t1 = 3,4 с ее скорость равна 5,9 м/с, в момент времени t2 = 6,1 с ее скорость равна 19,7 м/с. Чему равна скорость в момент времени t3 = 14,8 с? |
40 руб
оформление Word |
word | | 69059 |
Определить плотность энергии электрического поля, созданного в вакууме равномерно заряженной прямой длинной нитью с линейной плотностью заряда τ = 3·10–8 Кл/м, в точке, расположенной на расстоянии r0 = 10 cм от середины нити. |
43 руб
оформление Word |
word | | 69060 |
Вектор напряженности электрического поля в воде (ε1 = 81) вблизи границы со стеклом направлен под углом 60° к нормали. Найти угол между нормалью и направлением электрического поля в стекле, если диэлектрическая проницаемость в нем ε2 = 7. |
40 руб
оформление Word |
word | | 69061 |
В результате упругого рассеяния γ-кванта на свободном электроне первоначальная энергия фотона 0,1 МэВ уменьшилась на 16,3 кэВ. При этом оказалось, что импульс электрона отдачи в 2 раза больше импульса рассеянного фотона. В каком направлении движется электрон? |
46 руб
оформление Word |
word | | 69062 |
Найти частоты вращения электрона на первой орбите в атоме водорода и в ионе Не+. |
46 руб
оформление Word |
word | | 69063 |
Последовательный ряд радиоактивных распадов ядер, начинающийся с радия-226, включает в себя три α-превращения и два β-превращения. Какой изотоп, сколько и какие нейтрино при этом образуется? |
40 руб
оформление Word |
word | | 69064 |
Плоскопараллельная пластинка, абсолютный показатель преломления которой равен 1,5, освещается параллельным пучком монохроматического света с длиной волны 590 нм. Определите толщину пластинки, если максимальные значения интенсивности отраженного света соответствуют углам падения равным 30° и 34°. |
40 руб
оформление Word |
word | | 69065 |
Струя водяного пара при температуре 100 °С, направленная на глыбу льда, масса которой 5 кг и температура 0 °С, растопила ее и нагрела получившуюся воду до температуры 50 °С. Найти массу израсходованного пара и изменение энтропии при описанных процессах. |
40 руб
оформление Word |
word | | 69066 |
В сосуде емкостью 10 л находится 360 г водяного пара при температуре 470 К. Вычислить давление пара на стенки сосуда. Какую часть объема V составляет собственный объем V молекул пара? Какую часть давления р составляет внутреннее давление р'? |
40 руб
оформление Word |
word | | 69067 |
Взрыв водороднои? бомбы обусловлен очень быстрым энерговыделением, которое происходит в результате реакции ядерного синтеза тяжелых изотопов водорода: деи?терия и трития. В этои? реакции также образуются в частности неи?троны. Наи?ти количество неи?тронов, которые прои?дут через площадку в 1 см2, установленную перпендикулярно потоку этих частиц на расстоянии 1 км от эпицентра взрыва. Считать, что мощность бомбы эквивалентна 100 кт тротила, а удельное выделение энергии тротила составля |
57 руб
оформление Word |
word | | 69068 |
Камень брошен вертикально вверх со скоростью v0 = 10 м/с. На какой высоте h кинетическая энергия камня равна его потенциальной энергии? |
40 руб
оформление Word |
word | | 69069 |
Электрон, пройдя ускоряющую разность потенциалов попадает в однородное магнитное поле с индукцией В = 30 мТл. Траектория его движения представляет собой винтовую линию с радиусом R = 0,2 и шагом h = 2,1 мм. Определить ускоряющую разность потенциалов электрического поля. |
57 руб
оформление Word |
word | | 69070 |
За время t = 2 с вектор момента импульса материальной точки изменился от L1 до L2. Определить приложенный вектор момента силы, считая его постоянным.
 |
40 руб
оформление Word |
word | | 69071 |
Материальные точки имеют массы m1 = 1 кг, m2 = 2 кг, m3 = 3 кг. Силы взаимодействия между ними показаны на рисунке. Определить ускорение центра масс системы, состоящей из материальных точек массой m2 и m3.
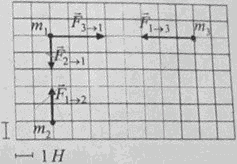 |
46 руб
оформление Word |
word | | 69072 |
Однородный сплошной цилиндр массой m1 = 1 кг может вращаться без трения вокруг оси симметрии. За эту ось он привязан к бруску массой m2 = 2 кг. К бруску приложена горизонтальная сила, равная 20 Н. Коэффициент трения бруска о плоскость равен 0,1. Определить ускорение цилиндра, если он катиться без проскальзывания.
 |
46 руб
оформление Word |
word | | 69073 |
Маховик в виде сплошного однородного цилиндра массой 2 кг и радиусом 20 см, вращаясь равнозамедленно, уменьшил частоту своего вращения с 480 об/мин до 120 об/мин и, при этом, сделал 40 оборотов. Определите работу торможения и тормозящий момент. |
40 руб
оформление Word |
word | | 69074 |
Маховик в виде однородного сплошного цилиндра, имеющего массу 2 кг и радиус 20 см, вращаясь равнозамедленно, уменьшил частоту своего вращения с 480 об/мин до 120 об/мин и, при этом, сделал 50 оборотов. Определите работу торможения и тормозящий момент. |
40 руб
оформление Word |
word | | 69075 |
Рабочим телом идеальной тепловой машины, работающей по циклу Карно, является идеальный газ. Исходное состояние его соответствует параметрам P1, V1, T1. Объем газа после изотермического расширения V2 = aV1, после адиабатического расширения — V3 = bV2.

Дано: газ — азот
Т1 = 420 К
Р1 = 2,1·105 Па
V1 = 2 л = 2·10–3 м3
a = 2,0
b = 1,6
Определить:
1. Количество молекул, находящихся в сосуде.
2. Характерные скорости молекул в исходном состоянии и после адиабатического расширения.
3. Энергию теплового движения молекул газа.
4. Среднюю энергию одной молекулы, энергию ее поступательного движения (при температуре Т1).
5. Теплоемкости газа при постоянном объеме и постоянном давлении.
6. Давление, температуру и объем газа в состояниях 2,3,4.
7. Изменение внутренней энергии газа в каждом процессе и за цикл.
8. Работу, совершенную газом за цикл и в каждом процессе.
9. Количество теплоты, полученное газом от нагревателя и отданное холодильнику.
10. КПД цикла как отношение совершенной работы к полученной энергии.
11. Изменение энтропии газа в каждом процессе и за весь цикл. Получить формулу КПД идеальной тепловой машины и вычислить по ней КПД цикла.
12. Построить диаграмму данного цикла (в масштабе) в координатах (P,V).
13. Определить значения коэффициентов диффузии, теплопроводности и вязкости данного газа в нормальных условиях и в исходном состоянии. |
230 руб
оформление Word |
word | | 69076 |
Рабочим телом идеальной тепловой машины, работающей по циклу Карно, является идеальный газ. Исходное состояние его соответствует параметрам P1, V1, T1. Объем газа после изотермического расширения V2 = aV1, после адиабатического расширения — V3 = bV2.

Дано: газ — аргон
Т1 = 420 К
Р1 = 2·105 Па
V1 = 2 л = 2·10–3 м3
a = 2,0
b = 1,8
Определить:
1. Количество молекул, находящихся в сосуде.
2. Характерные скорости молекул в исходном состоянии и после адиабатического расширения.
3. Энергию теплового движения молекул газа.
4. Среднюю энергию одной молекулы, энергию ее поступательного движения (при температуре Т1).
5. Теплоемкости газа при постоянном объеме и постоянном давлении.
6. Давление, температуру и объем газа в состояниях 2,3,4.
7. Изменение внутренней энергии газа в каждом процессе и за цикл.
8. Работу, совершенную газом за цикл и в каждом процессе.
9. Количество теплоты, полученное газом от нагревателя и отданное холодильнику.
10. КПД цикла как отношение совершенной работы к полученной энергии.
11. Изменение энтропии газа в каждом процессе и за весь цикл. Получить формулу КПД идеальной тепловой машины и вычислить по ней КПД цикла.
12. Построить диаграмму данного цикла (в масштабе) в координатах (P,V).
13. Определить значения коэффициентов диффузии, теплопроводности и вязкости данного газа в нормальных условиях и в исходном состоянии. |
230 руб
оформление Word |
word | | 69077 |
Рабочим телом идеальной тепловой машины, работающей по циклу Карно, является идеальный газ. Исходное состояние его соответствует параметрам P1, V1, T1. Объем газа после изотермического расширения V2 = aV1, после адиабатического расширения — V3 = bV2.

Дано: газ — аргон
Т1 = 420 К
Р1 = 2·105 Па
V1 = 1 л = 1·10–3 м3
a = 2,0
b = 1,8
Определить:
1. Количество молекул, находящихся в сосуде.
2. Характерные скорости молекул в исходном состоянии и после адиабатического расширения.
3. Энергию теплового движения молекул газа.
4. Среднюю энергию одной молекулы, энергию ее поступательного движения (при температуре Т1).
5. Теплоемкости газа при постоянном объеме и постоянном давлении.
6. Давление, температуру и объем газа в состояниях 2,3,4.
7. Изменение внутренней энергии газа в каждом процессе и за цикл.
8. Работу, совершенную газом за цикл и в каждом процессе.
9. Количество теплоты, полученное газом от нагревателя и отданное холодильнику.
10. КПД цикла как отношение совершенной работы к полученной энергии.
11. Изменение энтропии газа в каждом процессе и за весь цикл. Получить формулу КПД идеальной тепловой машины и вычислить по ней КПД цикла.
12. Построить диаграмму данного цикла (в масштабе) в координатах (P,V).
13. Определить значения коэффициентов диффузии, теплопроводности и вязкости данного газа в нормальных условиях и в исходном состоянии. |
230 руб
оформление Word |
word | | 69078 |
Рабочим телом идеальной тепловой машины, работающей по циклу Карно, является идеальный газ. Исходное состояние его соответствует параметрам P1, V1, T1. Объем газа после изотермического расширения V2 = aV1, после адиабатического расширения — V3 = bV2.

Дано: газ — водород
Т1 = 400 К
Р1 = 1,9·105 Па
V1 = 2 л = 2·10–3 м3
a = 2,0
b = 1,8
Определить:
1. Количество молекул, находящихся в сосуде.
2. Характерные скорости молекул в исходном состоянии и после адиабатического расширения.
3. Энергию теплового движения молекул газа.
4. Среднюю энергию одной молекулы, энергию ее поступательного движения (при температуре Т1).
5. Теплоемкости газа при постоянном объеме и постоянном давлении.
6. Давление, температуру и объем газа в состояниях 2,3,4.
7. Изменение внутренней энергии газа в каждом процессе и за цикл.
8. Работу, совершенную газом за цикл и в каждом процессе.
9. Количество теплоты, полученное газом от нагревателя и отданное холодильнику.
10. КПД цикла как отношение совершенной работы к полученной энергии.
11. Изменение энтропии газа в каждом процессе и за весь цикл. Получить формулу КПД идеальной тепловой машины и вычислить по ней КПД цикла.
12. Построить диаграмму данного цикла (в масштабе) в координатах (P,V).
13. Определить значения коэффициентов диффузии, теплопроводности и вязкости данного газа в нормальных условиях и в исходном состоянии. |
230 руб
оформление Word |
word | | 69079 |
Рабочим телом идеальной тепловой машины, работающей по циклу Карно, является идеальный газ. Исходное состояние его соответствует параметрам P1, V1, T1. Объем газа после изотермического расширения V2 = aV1, после адиабатического расширения — V3 = bV2.

Дано: газ — водород
Т1 = 400 К
Р1 = 1,9·105 Па
V1 = 1 л = 1·10–3 м3
a = 2,0
b = 1,8
Определить:
1. Количество молекул, находящихся в сосуде.
2. Характерные скорости молекул в исходном состоянии и после адиабатического расширения.
3. Энергию теплового движения молекул газа.
4. Среднюю энергию одной молекулы, энергию ее поступательного движения (при температуре Т1).
5. Теплоемкости газа при постоянном объеме и постоянном давлении.
6. Давление, температуру и объем газа в состояниях 2,3,4.
7. Изменение внутренней энергии газа в каждом процессе и за цикл.
8. Работу, совершенную газом за цикл и в каждом процессе.
9. Количество теплоты, полученное газом от нагревателя и отданное холодильнику.
10. КПД цикла как отношение совершенной работы к полученной энергии.
11. Изменение энтропии газа в каждом процессе и за весь цикл. Получить формулу КПД идеальной тепловой машины и вычислить по ней КПД цикла.
12. Построить диаграмму данного цикла (в масштабе) в координатах (P,V).
13. Определить значения коэффициентов диффузии, теплопроводности и вязкости данного газа в нормальных условиях и в исходном состоянии. |
230 руб
оформление Word |
word | | 69080 |
Рабочим телом идеальной тепловой машины, работающей по циклу Карно, является идеальный газ. Исходное состояние его соответствует параметрам P1, V1, T1. Объем газа после изотермического расширения V2 = aV1, после адиабатического расширения — V3 = bV2.

Дано: газ — кислород
Т1 = 400 К
Р1 = 1,8·105 Па
V1 = 2 л = 2·10–3 м3
a = 2,0
b = 1,6
Определить:
1. Количество молекул, находящихся в сосуде.
2. Характерные скорости молекул в исходном состоянии и после адиабатического расширения.
3. Энергию теплового движения молекул газа.
4. Среднюю энергию одной молекулы, энергию ее поступательного движения (при температуре Т1).
5. Теплоемкости газа при постоянном объеме и постоянном давлении.
6. Давление, температуру и объем газа в состояниях 2,3,4.
7. Изменение внутренней энергии газа в каждом процессе и за цикл.
8. Работу, совершенную газом за цикл и в каждом процессе.
9. Количество теплоты, полученное газом от нагревателя и отданное холодильнику.
10. КПД цикла как отношение совершенной работы к полученной энергии.
11. Изменение энтропии газа в каждом процессе и за весь цикл. Получить формулу КПД идеальной тепловой машины и вычислить по ней КПД цикла.
12. Построить диаграмму данного цикла (в масштабе) в координатах (P,V).
13. Определить значения коэффициентов диффузии, теплопроводности и вязкости данного газа в нормальных условиях и в исходном состоянии. |
230 руб
оформление Word |
word | | 69081 |
Рабочим телом идеальной тепловой машины, работающей по циклу Карно, является идеальный газ. Исходное состояние его соответствует параметрам P1, V1, T1. Объем газа после изотермического расширения V2 = aV1, после адиабатического расширения — V3 = bV2.

Дано: газ — гелий
Т1 = 450 К
Р1 = 1,7·105 Па
V1 = 2 л = 2·10–3 м3
a = 2,0
b = 1,6
Определить:
1. Количество молекул, находящихся в сосуде.
2. Характерные скорости молекул в исходном состоянии и после адиабатического расширения.
3. Энергию теплового движения молекул газа.
4. Среднюю энергию одной молекулы, энергию ее поступательного движения (при температуре Т1).
5. Теплоемкости газа при постоянном объеме и постоянном давлении.
6. Давление, температуру и объем газа в состояниях 2,3,4.
7. Изменение внутренней энергии газа в каждом процессе и за цикл.
8. Работу, совершенную газом за цикл и в каждом процессе.
9. Количество теплоты, полученное газом от нагревателя и отданное холодильнику.
10. КПД цикла как отношение совершенной работы к полученной энергии.
11. Изменение энтропии газа в каждом процессе и за весь цикл. Получить формулу КПД идеальной тепловой машины и вычислить по ней КПД цикла.
12. Построить диаграмму данного цикла (в масштабе) в координатах (P,V).
13. Определить значения коэффициентов диффузии, теплопроводности и вязкости данного газа в нормальных условиях и в исходном состоянии. |
230 руб
оформление Word |
word | | 69082 |
Рабочим телом идеальной тепловой машины, работающей по циклу Карно, является идеальный газ. Исходное состояние его соответствует параметрам P1, V1, T1. Объем газа после изотермического расширения V2 = aV1, после адиабатического расширения — V3 = bV2.

Дано: газ — азот гелий
Т1 = 450 К
Р1 = 1,7·105 Па
V1 = 1 л = 1·10–3 м3
a = 2,0
b = 1,6
Определить:
1. Количество молекул, находящихся в сосуде.
2. Характерные скорости молекул в исходном состоянии и после адиабатического расширения.
3. Энергию теплового движения молекул газа.
4. Среднюю энергию одной молекулы, энергию ее поступательного движения (при температуре Т1).
5. Теплоемкости газа при постоянном объеме и постоянном давлении.
6. Давление, температуру и объем газа в состояниях 2,3,4.
7. Изменение внутренней энергии газа в каждом процессе и за цикл.
8. Работу, совершенную газом за цикл и в каждом процессе.
9. Количество теплоты, полученное газом от нагревателя и отданное холодильнику.
10. КПД цикла как отношение совершенной работы к полученной энергии.
11. Изменение энтропии газа в каждом процессе и за весь цикл. Получить формулу КПД идеальной тепловой машины и вычислить по ней КПД цикла.
12. Построить диаграмму данного цикла (в масштабе) в координатах (P,V).
13. Определить значения коэффициентов диффузии, теплопроводности и вязкости данного газа в нормальных условиях и в исходном состоянии. |
230 руб
оформление Word |
word | | 69083 |
Рабочим телом идеальной тепловой машины, работающей по циклу Карно, является идеальный газ. Исходное состояние его соответствует параметрам P1, V1, T1. Объем газа после изотермического расширения V2 = aV1, после адиабатического расширения — V3 = bV2.

Дано: газ — воздух
Т1 = 450 К
Р1 = 1,6·105 Па
V1 = 2 л = 2·10–3 м3
a = 2,0
b = 1,8
Определить:
1. Количество молекул, находящихся в сосуде.
2. Характерные скорости молекул в исходном состоянии и после адиабатического расширения.
3. Энергию теплового движения молекул газа.
4. Среднюю энергию одной молекулы, энергию ее поступательного движения (при температуре Т1).
5. Теплоемкости газа при постоянном объеме и постоянном давлении.
6. Давление, температуру и объем газа в состояниях 2,3,4.
7. Изменение внутренней энергии газа в каждом процессе и за цикл.
8. Работу, совершенную газом за цикл и в каждом процессе.
9. Количество теплоты, полученное газом от нагревателя и отданное холодильнику.
10. КПД цикла как отношение совершенной работы к полученной энергии.
11. Изменение энтропии газа в каждом процессе и за весь цикл. Получить формулу КПД идеальной тепловой машины и вычислить по ней КПД цикла.
12. Построить диаграмму данного цикла (в масштабе) в координатах (P,V).
13. Определить значения коэффициентов диффузии, теплопроводности и вязкости данного газа в нормальных условиях и в исходном состоянии. |
230 руб
оформление Word |
word | | 69084 |
Рабочим телом идеальной тепловой машины, работающей по циклу Карно, является идеальный газ. Исходное состояние его соответствует параметрам P1, V1, T1. Объем газа после изотермического расширения V2 = aV1, после адиабатического расширения — V3 = bV2.

Дано: газ — воздух
Т1 = 450 К
Р1 = 1,6·105 Па
V1 = 1 л = 1·10–3 м3
a = 2,0
b = 1,8
Определить:
1. Количество молекул, находящихся в сосуде.
2. Характерные скорости молекул в исходном состоянии и после адиабатического расширения.
3. Энергию теплового движения молекул газа.
4. Среднюю энергию одной молекулы, энергию ее поступательного движения (при температуре Т1).
5. Теплоемкости газа при постоянном объеме и постоянном давлении.
6. Давление, температуру и объем газа в состояниях 2,3,4.
7. Изменение внутренней энергии газа в каждом процессе и за цикл.
8. Работу, совершенную газом за цикл и в каждом процессе.
9. Количество теплоты, полученное газом от нагревателя и отданное холодильнику.
10. КПД цикла как отношение совершенной работы к полученной энергии.
11. Изменение энтропии газа в каждом процессе и за весь цикл. Получить формулу КПД идеальной тепловой машины и вычислить по ней КПД цикла.
12. Построить диаграмму данного цикла (в масштабе) в координатах (P,V).
13. Определить значения коэффициентов диффузии, теплопроводности и вязкости данного газа в нормальных условиях и в исходном состоянии. |
230 руб
оформление Word |
word |
|