| № |
Условие |
Решение
|
Наличие |
| 60415 |
Амперметр на 10 А, шкала которого имеет 100 делений, включен через трансформатор тока 500/5 А. Показания амперметра 42 деления. Определить ток в первичной цепи трансформатора. |
40 руб
оформление Word |
word |
| 60416 |
200 м проволоки сечением 4 мм2 имеют сопротивление 6,5 Ом. Определить материал проводника. |
40 руб
оформление Word |
word |
| 60417 |
Набухшее бревно, сечение которого постоянно по всей длине, погрузилось вертикально в воду так, что над водой находится лишь малая (по сравнению с длиной) его часть. Период Т колебаний бревна равен 5 с. Определить длину l бревна. |
40 руб
оформление Word |
word |
| 60418 |
Амплитуда затухающих колебаний маятника за время t1 = 5 мин уменьшилась в два раза. За какое время t2, считая от начального момента, амплитуда уменьшится в восемь раз? |
40 руб
оформление Word |
word |
| 60419 |
За время t = 8 мин амплитуда затухающих колебаний маятника уменьшилась в три раза. Определить коэффициент затухания δ. |
40 руб
оформление Word |
word |
| 60420 |
Амплитуда колебаний маятника длиной l = 1 м за время t = 10 мин уменьшилась в два раза. Определить логарифмический декремент колебаний θ. |
40 руб
оформление Word |
word |
| 60421 |
Для электрической схемы определить наиболее рациональным методом токи в ветвях, напряжение на каждом элементе, мощность элементов и приемника в целом, режимы работы источников, их мощность, ток в одной из ветвей, пользуясь методом эквивалентного генератора. Параметры элементов схемы следующие: Е1 = 30 В; E6 = 0 В; E7 = 0 В; Е8 = 20 В; R1 = 2,0 Ом; R2 = 0 Ом; R3 = 1,8 Ом; R4 = ∞ Ом; R5 = 1,0 Ом; R6 = 0 Ом; R7 = 1,2 Ом; R8 = 1,6 Ом.
 |
80 руб
оформление Word |
word |
| 60422 |
Определить силу тока в обмотке, состоящей из 50 витков, намотанной на магнитопровод со средней длиной l = 20 см, если сечение магнитопровода 9 см2, μ = 15·103 и индукция В = 0,3 Тл. |
40 руб
оформление Word |
word |
| 60423 |
Тело массой 5 г совершает затухающие колебания. В течение 50 с тело потеряло 60 % своей энергии. Определить коэффициент сопротивления b. |
40 руб
оформление Word |
word |
| 60424 |
Определить период Т затухающих колебаний, если период Т0 собственных колебаний системы равен 1 с и логарифмический декремент затухания θ = 0,628. |
40 руб
оформление Word |
word |
| 60425 |
Найти число N полных колебаний системы, в течение которых энергия системы уменьшилась в n = 2 раза. Логарифмический декремент колебаний θ = 0,01. |
40 руб
оформление Word |
word |
| 60426 |
На железнодорожной платформе установлено орудие, жестко скрепленное с платформой. Масса платформы и орудия М = 21 т. Орудие производит выстрел по углом φ = 60° к линии горизонта в направлении пути. Какую скорость приобретает платформа с орудием вследствие отдачи, если масса снаряда m = 51 кг и он вылетает из канала ствола со скоростью v1 = 501 м/с? |
40 руб
оформление Word |
word |
| 60427 |
Тонкий стержень массой m = 1,7 кг и длиной L = 1,7 м вращается вокруг оси, перпендикулярной к его длине и проходящей через точку стержня, находящуюся на расстоянии L1 = 0,17 м от одного из концов. Частота вращения стержня n = 1,7 с–1. Определить его кинетическую энергию. |
40 руб
оформление Word |
word |
| 60428 |
Естественный свет падает нормально на пластину оконного стекла (n = 1,5). Какая часть светового потока пройдет через стекло? |
40 руб
оформление Word |
word |
| 60429 |
Колебательная система совершает затухающие колебания с частотой ν = 1000 Гц. Определить частоту ν0 собственных колебаний, если резонансная частота νpeз = 998 Гц. |
40 руб
оформление Word |
word |
| 60430 |
Определить, на сколько резонансная частота отличается от частоты ν0 = 1 кГц собственных колебаний системы, характеризуемой коэффициентом затухания δ = 400 с–1. |
40 руб
оформление Word |
word |
| 60431 |
Определить логарифмический декремент колебаний θ колебательной системы, для которой резонанс наблюдается при частоте, меньшей собственной частоты ν0 = 10 кГц на Δν = 2 Гц. |
40 руб
оформление Word |
word |
| 60432 |
Период Т0 собственных колебаний пружинного маятника равен 0,55 с. В вязкой среде период Т того же маятника стал равным 0,56 с. Определить резонансную частоту νрез колебаний. |
40 руб
оформление Word |
word |
| 60433 |
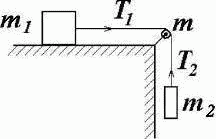
В установке известны масса блока (однородного сплошного цилиндра) m = 10 г и его радиус R = 3 см, а также массы тел m1 = 13 г и m2 = 8 г. Скольжения нити и трения в оси блока и с поверхностью стола нет. Найти угловое ускорение блока и отношения натяжений Т1 к Т2 нити в процессе движения.
 |
40 руб
оформление Word |
word |
| 60434 |
На двух параллельный проводниках, находящихся под углом α = 30° к горизонту, находится металлический стержень массой m = 40 г. Расстояние между проводниками d = 0,5 м. С каким ускорением и в каком направлении будет скользить стержень по проводникам, если вся система находитсся в магнитном поле с индукцией B = 0,5 Тл, направленным вертикально вниз, а по проводнику пропускают ток I = 10 А? Трением пренебречь. |
51 руб
оформление Word |
word |
| 60435 |
Стержень массой 3 кг и длиной 1,5 м вращается вокруг оси, проходящей через один из его концов, по закону φ = 6+4t+2t2. Определить момент силы, действующей на другой его конец. |
40 руб
оформление Word |
word |
| 60436 |
К спиральной пружине жесткостью k = 10 Н/м подвесили грузик массой m = 10 г и погрузили всю систему в вязкую среду. Приняв коэффициент сопротивления b равным 0,1 кг/с, определить: 1) частоту ν0 собственных колебаний; 2) резонансную частоту νpез; 3) резонансную амплитуду Aрез, если вынуждающая сила изменяется по гармоническому закону и ее амплитудное значение F0 = 0,02 Н; 4) отношение резонансной амплитуды к статическому смещению под действием |
40 руб
оформление Word |
word |
| 60437 |
Во сколько раз амплитуда вынужденных колебаний будет меньше резонансной амплитуды, если частота изменения вынуждающей силы будет больше резонансной частоты: 1) на 10 %? 2) в два раза? Коэффициент затухания δ в обоих случаях принять равным 0,1ω0 (ω0 — угловая частота собственных колебаний). |
46 руб
оформление Word |
word |
| 60438 |
Задано уравнение плоской волны ξ(х,t) = Acos(ωt–kx), где A = 0,5 см, ω = 628c–1, k = 2 м–1. Определить: 1) частоту колебаний ν и длину волны λ ; 2) фазовую скорость θ; 3) максимальные значения скорости  max и ускорения max и ускорения  max колебаний частиц среды. max колебаний частиц среды. |
40 руб
оформление Word |
word |
| 60439 |
Показать, что выражение ξ(х,t) = Acos(ωt–kx) удовлетворяет волновому уравнению 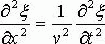 при условии, что ω = kv. при условии, что ω = kv. |
40 руб
оформление Word |
word |
| 60440 |
Три точечных заряда +1 нКл, –1 нКл и +1 нКл соответственно расположены в вершинах квадрата со стороной 1 см. Вычислите напряжённость и потенциал электрического поля в вершине, где отсутствует заряд. Постройте вектор напряжённости поля на чертеже. |
40 руб
оформление Word |
word |
| 60441 |
Точка совершает одновременно два колебания, происходящих по взаимно перпендикулярным направлениям и выражаемых уравнениями x = 8cosπt, y = 8cosπ(t+1) (длина в сантиметрах, время в секундах). Найти уравнение траектории и построить график её движения. |
40 руб
оформление Word |
word |
| 60442 |
Плоская звуковая волна имеет период Т = 3 мс, амплитуду A = 0,2 мм и длину волны λ = 1,2 м. Для точек среды, удаленных от источника колебаний на расстояние х = 2 м, найти: 1) смещение ξ(х,t) в момент t = 7 мс; 2) скорость  и ускорение и ускорение  для того же момента времени. Начальную фазу колебаний принять равной нулю. для того же момента времени. Начальную фазу колебаний принять равной нулю. |
40 руб
оформление Word |
word |
| 60443 |
От источника колебаний распространяется волна вдоль прямой линии. Амплитуда A колебаний равна 10 см. Как велико смещение точки, удаленной от источника на х = 3/4λ, в момент, когда от начала колебаний прошло время t = 0,9Т? |
40 руб
оформление Word |
word |
| 60444 |
Волна с периодом Т = 1,2 с и амплитудой колебаний A = 2 см распространяется со скоростью θ = 15 м/с. Чему равно смещение ξ(х,t) точки, находящейся на расстоянии x = 45 м от источника волн, в тот момент, когда от начала колебаний источника прошло время t = 4 с? |
40 руб
оформление Word |
word |