VI Варианты 6.1 - 6.3

      Предприятие выпускает 4 вида продукции, используя два вида сырья в пределах выделенных фондов В1 и В2. Нормы расхода сырья на единицу продукции приведены в табл. 8. Зависимость прибыли от объема производства каждого вида продукции задана аналитически (табл. 9). Определить оптимальный план производства, рассматривая выпуск продукции только в целых единицах.

VII Варианты 7.1 - 7.3

      Требуется распределить имеющиеся средства в количестве R единиц по предприятиям и годам планового периода. ; ; ji(x)=[ bi x]. Квадратные скобки означают взятие целого по правилам округления. Значения всех параметров даны в табл. 10 и 11.

VIII Варианты 8.1 - 8.3

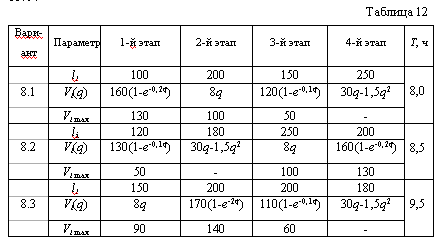
      Автомобиль должен пройти 4 этапа длиной li (км) каждый. Известны зависимости скорости движения автомобиля V (км/ч) от расхода горючего q (л/км) для каждого этапа. Скорость движения на трех этапах ограничена сверху. Соответствующие данные приведены в табл. 12. Необходимо определить скорости движения, обеспечивающие минимальный расход горючего при заданном времени пробега Т (ч). Показать, как изменится решение при увеличении или уменьшении Т на 10% .

IX Варианты 9.1 - 9.3

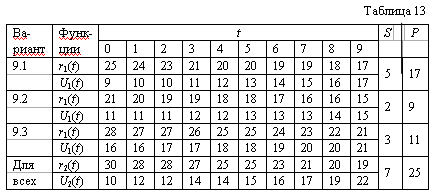
      Характеристики оборудования зависят от его возраста t: r(t) - стоимость ежегодно производимой продукции; U(t) - годовые эксплуатационные затраты; S(t) - остаточная стоимость (выручка от продажи оборудования). На начало планового периода из N лет работающее оборудование имеет возраст t=t0. В начале любого года оборудование можно сохранить или продать и купить новое. Продолжительность замены много меньше года. Пусть - число лет с начала планового периода. Тогда при <5 оборудование может заменяться новым, такого же типа с характеристиками r1(t), U1(t), S1(t) и ценой Р1, а при 5 может заменяться таким же либо другого типа с характеристиками r2(t), U2(t), S2(t) и ценой Р2. Необходимо определить оптимальную политику замены оборудования для N=9 и t0=0?6. Исходные данные приведены в табл.13. .

X Варианты 10.1 - 10.3

      Планируется деятельность объединения, включающего 2 предприятия, на 4 года. Известны функции дохода i-го предприятия в j-м году gij(xij), где хij - количество ресурса, вкладываемое в i-е предприятие в j-м году. Вложенные ресурсы за год уменьшаются до величины ji(x). Оставшийся в конце года ресурс возвращается в централизованный фонд объединения и снова полностью распределяется. Определить оптимальное распределение ресурсов по предприятиям и годам, если начальный централизованный фонд ресурсов равен R, а зависимости имеют вид: ; ; . Квадратные скобки означают взятие целого по правилам округления. Значения коэффициентов и R даны в табл. 14, 15. .