САиИО (ТПР)
Динамическое программирование / (Условия задач 11-15)
XI Варианты 11.1 - 11.3
Пусть непилотируемый летательный аппарат, запускаемый с земли, должен за время Т, кратное dt, достигнуть высоты Н. Сигнал коррекции траектории поступает через интервалы dt и мгновенно отрабатывается. Между корректировками полет идет под одним углом к горизонту. Известны зависимости:
; ,
где q - расход горючего, кг/с; h - высота аппарата относительно земли, м; v - скорость полета, км/ч; a - угол подъема (спуска), град;
Требуется найти оптимальную траекторию полета с точностью не хуже 4% от Н и соответствующее ей (оптимальное) значение Т; построить графики траектории в координатах “высота - время” и “высота - расстояние по земле от точки старта”.
Значения параметров приведены в табл. 16. |
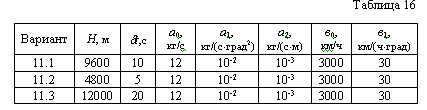 |
XII Варианты 12.1 - 12.3
На кондитерской фабрике организуется выпуск трех видов продукции из двух видов сырья. Известны нормы расхода сырья на изготовление единицы продукции и количество имеющегося сырья (табл. 17). Зависимость прибыли от объема производства каждого вида продукции дана в табл. 18.
Требуется определить оптимальный план производства продукции.
Указание: использовать прием снижения размерности на основе множителей Лагранжа. |
 |
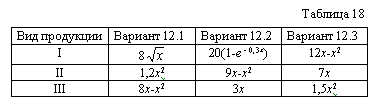 |
XIII Варианты 13.1 - 13.3
Два вида средств в количестве P и Q, выделенных предприятию на квартал, необходимо распределить по месяцам. Прибыль за месяц зависит от величины использованных средств, как показано в табл. 19, где х и у - количества 1-го и 2-го вида средств, используемых в соответствующий месяц. На каждый месяц должно быть выделено не менее одной единицы первого вида средств.
Указание: использовать прием снижения размерности на основе множителей Лагранжа. При этом невязка по сумме средств не должна быть больше 3%.
|
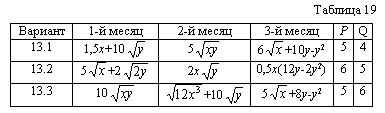 |
XIV Варианты 14.1 - 14.3
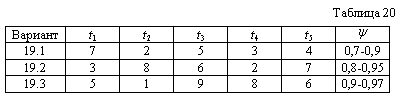
Обработка информации осуществляется пятью последовательно включенными вычислительными устройствами (ВУ). Известна продолжительность однократного счета на каждом из ВУ - ti (табл. 20). Для повышения достоверности обработки применяется повторный счет на отдельных ВУ. Зависимость вероятности получения правильного результата от числа повторностей счета Р(к) дана в аналитическом виде (табл. 21).
Определить вариант обработки информации, обеспечивающий вероятность получения правильного результата не хуже за минимальное время счета.
Вывести функциональное уравнение для случая максимизации при заданном общем времени счета.
. |
 |
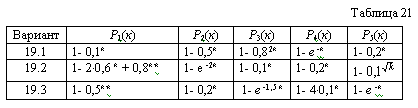 |
XV Варианты 15.1 - 15.3
Проектируется строительство дороги с четырьмя перегонами (табл. 22). Капитальные (приведенные) и эксплуатационные затраты зависят от длины перегона li: с уменьшением li первые возрастают из-за увеличения объема земляных работ, а вторые снижаются .
Спроектировать дорогу общей длиной не более L с минимальными затратами.
Записать функциональное уравнение для случая минимизации длины при заданном уровне затрат.
Примечание: для упрощения расчетов считать, что эксплуатационные затраты даны на весь период эксплуатации дороги. |
|