XVI Варианты 16.1 - 16.3

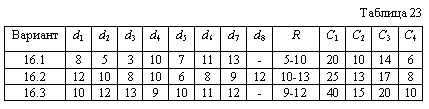
      На период в Т дней известен объем погрузочно-разгрузочных работ, выражаемый в ежедневной потребности в рабочих - dt, t=1,..,T (табл. 23). Рабочих можно ежедневно нанимать и увольнять. При нехватке рабочих прибегают к сверхурочным работам и затраты возрастают на С1 за каждого недостающего рабочего, расходы на содержание одного незанятого рабочего составляют С2, а на найм одного рабочего - С3. Увольнение требует расходов С9. Составить оптимальный план регулирования численности рабочих на Т дней, если исходное количество рабочих равно R.

XVII Варианты 17.1 - 17.3

      Пусть непилотируемый летательный аппарат, запускаемый с земли, должен за время Т, кратное dt, достигнуть высоты Н. Сигнал коррекции траектории поступает через интервалы dt и мгновенно отрабатывается. Между корректировками полет идет под одним углом к горизонту. Известны зависимости: q=a0+a1a2-a2h, v=b0-b1a, где q - расход горючего, кг/с; h - высота аппарата относительно земли, м; v - скорость полета, км/ч; a - угол подъема (спуска), град. Значения всех величин приведены в табл. 24 Определить оптимальную траекторию полета с точностью не хуже 4% от Н, построить графики траекторий в координатах “высота - время” и “высота - расстояние по земле от точки старта”.

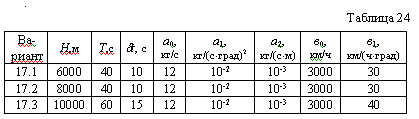XVIII Варианты 18.1 - 18.3

      Для восстановления дороги проводятся текущие и капитальные ремонты. Ремонт может производиться не более 1 раза в год и только в начале года (длительность ремонта много меньше года). Текущий ремонт требует Ст затрат, а капитальный - Ск (табл. 25). После текущего ремонта годовые эксплуатационные затраты равны , а после капитального - , где t - число лет, прошедшее после ремонта на начало рассматриваемого года. Определить оптимальный план ремонта дороги на Т лет, если на начало этого периода прошло лет после текущего (капитального) ремонта.

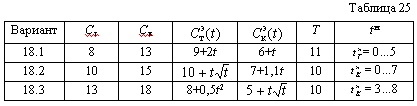XIX Варианты 19.1 - 19.3

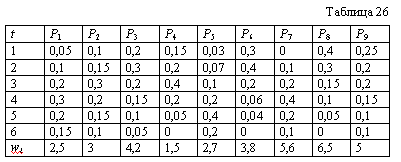
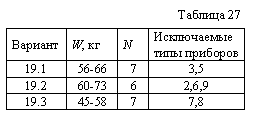
      На космическом корабле действует N различных приборов. Прибор типа i весит wi кг, а суммарный вес приборов не должен превышать W кг. Известны вероятности Рi(t), с которыми i-й прибор может функционировать в течение t единиц времени (табл. 26). Как только запас какого-либо типа прибора станет равным нулю, космический корабль должен вернуться на Землю. Число приборов и их максимальный суммарный вес даны в табл. 27. Определить запасы приборов, обеспечивающие наибольшее математическое ожидание времени полета космического корабля. .

XX Варианты 20.1 - 20.3

      Продукты доставляются на грузовике с полезным объемом V. Потребность в I видах продуктов описывается непрерывным равномерным распределением с плотностью где mi - масса i-го продукта. Единица массы продукта i занимает объем vi (табл. 28). Определить, как загрузить грузовик, чтобы минимизировать математическое ожидание неудовлетворенного за рейс спроса. Как изменится решение, если потребовать минимизации нереализованной стоимости при известной цене продуктов Сi, руб/кг. С1=1,5; С2=3,2; С3=0,8; С4=2,5. Примечание: рассматривать только целые значения массы продукта.