Движение микрочастиц

• Вероятность dW обнаружить частицу в интервале от х до x + dx (в одномерном случае) выражается формулой

dW=|ψ(x)|²dx

где [ψ(x)]²— плотность вероятности.

Вероятность W обнаружить частицу в интервале от х₁ до х₂ находится интегрированием dW в указанных пределах

$W={\int }_{x_1}^{x_2}{\left|\psi \left(x\right)\right|}^{2}dx$

• Собственное значение энергии Еn частицы, находящейся на n-м энергетическом уровне в бесконечно глубоком одномерном прямоугольном потенициальеом ящике, определяется формулой

$E_n=\frac{{\mathrm{\pi }}^2{\mathrm{ħ}}^2}{2m{l}^2}{n}^2$

(n = 1, 2, 3, …)

где l — ширина потенциального ящика.

Соответствующая этой энергии собственная волновая функция имеет вид

${\psi }_n\left(x\right)=\sqrt{\frac{2}{l}}\sin \frac{\mathrm{\pi n}}{l}x$

• Коэффициент преломления n волн де Бройля на границе низкого потенциального барьера бесконечной ширины (рисунок) U₀<E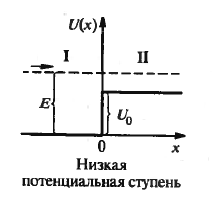



$n=\frac{{\lambda }_1}{{\lambda }_2}=\frac{k_1}{k_2}$

где λ₁ и λ₂ — длины волн де Бройля в областях I и II (частица движется из области I во II);

k₁ — k₂ — соответствующие значения волновых чисел.

• Коэффициенты отражения ρ и пропускания τ волн де Бройля через низкий (U<=E) потенциальный барьер бесконечной ширины

$\rho ={\left|\frac{k_1-k_2}{k_1+k_2}\right|}^2$

$\tau =\frac{4k_1{k}_2}{{\left(k_1+k_2\right)}^2}$

где k₁ и k₂ — волновые числа волн де Бройля в областях I и II.

• Коэффициент прозрачности D прямоугольного потенциального барьера конечной ширины

$D\approx exp\left(-\frac{4\pi }{h}\sqrt{2\left(U_0-E\right)}d\right)$

где

U — высота потенциального барьера
Е — энергия частицы
d — ширина барьера