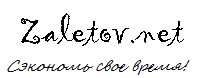Механические колебания. Основные формулы

Колеба́ния — повторяющийся в той или иной степени во времени процесс изменения состояний системы около точки равновесия.

Гармонические колебания — колебания, при которых физическая величина изменяется с течением времени по гармоническому (синусоидальному, косинусоидальному) закону. • Уравнение гармонического колебания имеет вид

$x=A\cos \left(\omega t+{\phi }_0\right)$

где х — отклонение колеблющейся величины в текущий момент времени t от среднего за период значения (например, в кинематике — смещение, отклонение колеблющейся точки от положения равновесия);

А — амплитуда колебания, т.е. максимальное за период отклонение колеблющейся величины от среднего за период значения, размерность A совпадает с размерностью x;

ω (радиан/с, градус/с) — циклическая частота, показывающая, на сколько радиан (градусов) изменяется фаза колебания за 1 с;

$\omega t+{\phi }_0$ — полная фаза колебания (сокращённо — фаза, не путать с начальной фазой);

${\phi }_0$ — начальная фаза колебаний, которая определяет значение полной фазы колебания (и самой величины x) в момент времени t = 0.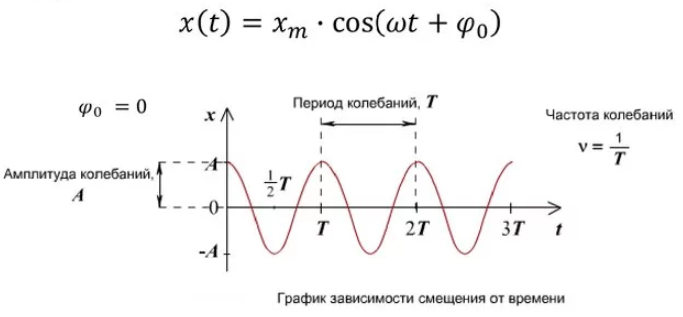



• В круговых или циклических процессах вместо характеристики «частота» используется понятие круговая (циклическая) частота ω (рад/с, Гц, с−1), показывающая число колебаний за 2π единиц времени:

$\omega =\frac{2\pi }{T}$

или $\omega =2\pi \nu$

где ν и T -частота и период колебаний.

• Скорость точки, совершающей гармонические колебания:

$V=\frac{dx}{dt}=-A\omega \sin (\omega t+{\phi }_0)$

• Ускорение точки, совершающей гармонические колебания:

$a=\frac{dV}{dt}=-A{\omega }^2\cos (\omega t+{\phi }_0)$

• Амплитуда А результирующего колебания, полученного при сложении двух колебаний с одинаковыми частотами, происходящих по одной прямой, определяется по формуле

$A^2=A_1^2+A_2^2+2A_1{A}_2\cos ({\phi }_2-{\phi }_1)$

где A1 и А2— амплитуды составляющих колебаний; φ1 и φ2— их начальные фазы.

• Начальная фаза φ результирующего колебания может быть найдена из формулы

$tg\phi =\frac{A_1\sin {\phi }_1+A_2\sin {\phi }_2}{A_1\cos {\phi }_1+A_2\cos {\phi }_2}$


Примеры задач:

Написать уравнение гармонического колебательного движения с амплитудой..
Точка совершает гармоническое колебание. Период..