Теорема Гюйгенса — Штейнера

Теорема Гюйгенса — Штейнера (теорема Гюйгенса, теорема Штейнера):

Момент инерции I тела относительно произвольной неподвижной оси равен сумме момента инерции этого тела I_C относительно параллельной ей оси, проходящей через центр масс тела, и произведения массы тела m на квадрат расстояния a между осями

$I=I_C+m{a}^2$

I — искомый момент инерции относительно параллельной оси,
I_C — известный момент инерции относительно оси, проходящей через центр масс тела,
m — масса тела,
a — расстояние между указанными осями.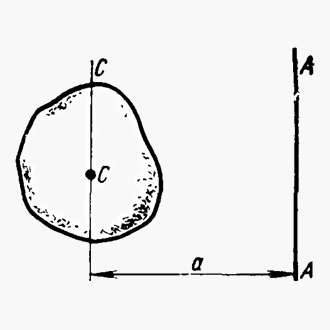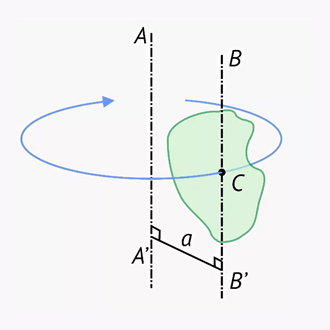

  

Теорема названа по имени швейцарского математика Якоба Штейнера и голландского математика, физика и астронома Христиана Гюйгенса.

Пример

Момент инерции стержня относительно оси C, проходящей через его центр и перпендикулярной стержню равен

$I_C=\frac{m{L}^2}{12}$

Тогда, согласно теореме Штейнера, его момент относительно произвольной параллельной оси будет равен

$I=I_C+m{a}^2$

где a — расстояние между этой осью и осью C.
В частности, момент инерции стержня относительно оси, проходящей через его конец и перпендикулярной стержню, можно найти, положив в последней формуле a = L/2:

$I=I_C+m{\left(\frac{L}{2}\right)}^2=\frac{m{L}^2}{12}+\frac{m{L}^2}{4}=\frac{m{L}^2}{3}$