Потенциал. Энергия зарядов. Работа

• Потенциал электрического поля есть величина, равная отношению потенциальной энергии точечного положительного заряда, помещенную в данную точку поля, к этому заряду;

$\phi =\frac{П}{Q}$

или потенциал электрического поля есть величина, равная отношению работы сил поля по перемещению точечного положительного заряда из данной точки поля в бесконечность к этому заряду:

$\phi =\frac{A}{Q}$

Потенциал электрического поля в бесконечности условно принят равным нулю.

Отметим, что при перемещении заряда в электрическом поле работа Aв.с внешних сил равна по модулю работе Aс.п сил поля и противоположна ей по знаку:

A_в.с.= –A_с.п.

• Потенциал электрического поля, создаваемый точечным зарядом Q на расстоянии r от заряда,

$\phi =\frac{Q}{4{\mathrm{\pi \epsilon \epsilon }}_0\mathrm{r}}$

• Потенциал электрического поля, создаваемого металлической, несущей заряд Q сферой радиусом R, на расстоянии гот центра сферы:

внутри сферы (r<R) ;

$\phi =\frac{Q}{4{\mathrm{\pi \epsilon \epsilon }}_0\mathrm{R}}$

на поверхности сферы (r=R)

$\phi =\frac{Q}{4{\mathrm{\pi \epsilon \epsilon }}_0\mathrm{R}}$

вне сферы (r>R) .

$\phi =\frac{Q}{4{\mathrm{\pi \epsilon \epsilon }}_0\mathrm{r}}$

Во всех приведенных для потенциала заряженной сферы формулах ε есть диэлектрическая проницаемость однородного безграничного диэлектрика, окружающего сферу.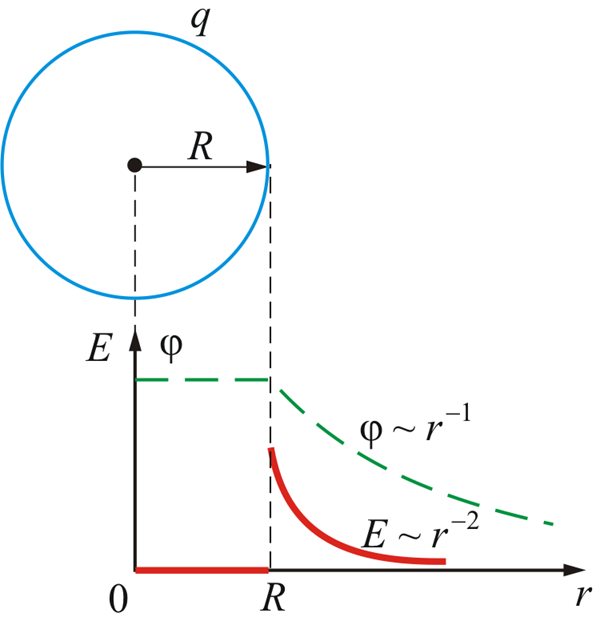



• Потенциал электрического поля, созданного системой n точечных зарядов, в данной точке в соответствии с принципом суперпозиции электрических полей равен алгебраической сумме потенциалов φ₁, φ₂, ... , φ_n, создаваемых отдельными точечными зарядами Q₁, Q₂, ..., Q_n:

$\phi =\underset{i=1}{\overset{n}{\sum {\phi }_i}}$

• Энергия W взаимодействия системы точечных зарядов Q₁, Q₂, ..., Q_n определяется работой, которую эта система зарядов может совершить при удалении их относительно друг друга в бесконечность, и выражается формулой

$W=\frac{1}{2}\underset{i=1}{\overset{n}{\sum Q_i{\phi }_i}}$,

где φ_i — потенциал поля, создаваемого всеми п–1 зарядами (за исключением 1-го) в точке, где расположен заряд Q_i .

• Потенциал связан с напряженностью электрического поля соотношением

Е= –gradφ.

В случае электрического поля, обладающего сферической симметрией, эта связь выражается формулой

$\overrightarrow{E}=-\frac{d\phi }{dr}\frac{\overrightarrow{r}}{r}$,

или в скалярной форме

$E=-\frac{d\phi }{dr}$

а в случае однородного поля, т. е. поля, напряженность которого в каждой точке его одинакова как по модулю, так и по направлению,

$E=\frac{{\phi }_1-{\phi }_2}{d}$,

где
φ₁ и φ₂ — потенциалы точек двух эквипотенциальных поверхностей;
d — расстояние между этими поверхностями вдоль электрической силовой линии.

• Работа, совершаемая электрическим полем при перемещении точечного заряда Q из одной точки поля, имеющей потенциал φ₁, в другую, имеющую потенциал φ₂,

A=Q(φ₁—φ₁), или $A=Q{\int }_L{E}_{l}dl$,

где E_l — проекция вектора напряженности Е на направление перемещения; dl — перемещение.

В случае однородного поля последняя формула принимает вид

A=QElcosα,

где l — перемещение; α — угол между направлениями вектора

В случае электростатического поля циркуляция вектора напряженности равна нулю: $\oint E_{l}dl=0$


Примеры задач:

Два шарика с зарядами q1=6,66 нКл и q1=13,33 нКл..
Найти потенциал φ точки поля, находящейся на расстоянии..